Appearance
动态规划
基础问题
509. 斐波那契数
js
/**
* v1 动态规划(自底向上)
* @param {number} n
* @return {number}
*/
let fib = function (n) {
if (n === 0 || n === 1) return n;
// dp table
let dp = new Array(n + 1).fill(0);
// base case
dp[0] = 0;
dp[1] = 1;
// 状态转移
for (let i = 2; i < n + 1; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};70. 爬楼梯
js
/**
* v1 动态规划(自顶向下)
* @param {number} n
* @return {number}
*/
const climbStairs = function (n) {
// 确定dp数组(dp table)以及下标的含义: 爬到第i层楼梯,有dp[i]种方法
// 确定递推公式: dp[i] = dp[i - 1] + dp[i - 2]
// dp数组如何初始化: dp[1] = 1 dp[2] = 2
// 确定遍历顺序: 从前向后
// 举例推导dp数组
const dp = new Array(n + 1);
dp[1] = 1;
dp[2] = 2;
for (let i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};746. 使用最小花费爬楼梯
js
/**
* v1 动态规划(自底向上)
*
* 时间复杂度:O(n)
* 空间复杂度:O(n)
* @param {number[]} cost
* @return {number}
*/
const minCostClimbingStairs = function (cost) {
// 1. dp数组和索引的定义
// 定义dp[i]表示到达第i个阶梯最低花费
// 2. 状态转移方程
// dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
// 3. 初始化
// 4. 遍历顺序
const n = cost.length;
// 定义dp[i]表示到达第i个阶梯最低花费
const dp = new Array(n + 1);
// 初始化
dp[0] = 0;
dp[1] = 0;
// 遍历顺序
for (let i = 2; i <= n; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
// 返回最低花费
return dp[n];
};62. 不同路径
js
/**
* v1 动态规划(自底向上)
* @param {number} m
* @param {number} n
* @return {number}
*/
const uniquePaths = function (m, n) {
// 1、 明确dp数组和索引的定义
// dp[i][j]表示从(0, 0)出发到达(i, j)的路径数, 结果:dp[m - 1][n - 1]
// 2、状态转移方程
// dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
// 3、初始化
// dp[0][j] = 1 dp[i][0] = 1
// 4、遍历顺序
// 先行后列或者先列后行都可以
const dp = Array.from({ length: m }, () => new Array(n).fill(1));
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
};63. 不同路径 II
js
/**
* v1 动态规划(自底向上)
*
* 时间复杂度:O(m * n)
* 空间复杂度:O(m * n)
* @param {number[][]} obstacleGrid
* @return {number}
*/
const uniquePathsWithObstacles = function (obstacleGrid) {
// 1、明确dp数组和索引的定义
// dp[i][j]表示从(0, 0)到(i , j)的不同路径数量,结果 dp[m - 1][n - 1]
// 2、状态转移方程
// 如果 obstacleGrid[i][j] !== 1
// dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
// 3、初始化
// 4、遍历顺序
const m = obstacleGrid.length;
const n = obstacleGrid[0].length;
const dp = Array.from({ length: m }, () => new Array(n).fill(0));
// 初始化
// 初始化第一列
for (let i = 0; i < m; i++) {
// 如果出现障碍,则后续位置无法到达(起点也有可能)
if (obstacleGrid[i][0] === 1) {
break;
}
dp[i][0] = 1;
}
// 初始化第一行
for (let j = 0; j < n; j++) {
// 如果出现障碍,则后续位置无法到达(起点也有可能)
if (obstacleGrid[0][j] === 1) {
break;
}
dp[0][j] = 1;
}
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
// 如果当前节点是障碍则路径为默认值0
if (obstacleGrid[i][j] === 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
};64. 最小路径和
js
/**
* v1 动态规划(dp数组)
* @param {number[][]} grid
* @return {number}
*/
let minPathSum = function (grid) {
let m = grid.length;
let n = grid[0].length;
// dp[i][j]表示从起点出发到达grid[i][j]的最小数字总和
const dp = Array.from({ length: m }, () => new Array(n).fill(Infinity));
// 初始化
let sum = 0;
for (let i = 0; i < m; i++) {
sum += grid[i][0];
dp[i][0] = sum;
}
sum = 0;
for (let i = 0; i < n; i++) {
sum += grid[0][i];
dp[0][i] = sum;
}
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
// 当前位置的状态由左边和上边位置构成
dp[i][j] =
Math.min(
dp[i - 1][j], // 左边
dp[i][j - 1] // 上边
) + grid[i][j];
}
}
return dp[m - 1][n - 1];931. 下降路径最小和
js
/**
* v1 动态规划(dp数组)
* @param {number[][]} matrix
* @return {number}
*/
let minFallingPathSum = function (matrix) {
let n = matrix.length;
let res = Number.MAX_SAFE_INTEGER;
// 定义:dp[i][j]表示从第一行到matrix[i][j]最小下降路径和
let dp = Array.from({ length: n }, () => new Array(n));
// 初始化
for (let i = 0; i < n; i++) {
dp[0][i] = matrix[0][i];
}
for (let i = 1; i < n; i++) {
for (let j = 0; j < n; j++) {
// 处理边界情况
let top = dp[i - 1][j];
let topLeft = j - 1 >= 0 ? dp[i - 1][j - 1] : Number.MAX_SAFE_INTEGER;
let topRight = j + 1 < n ? dp[i - 1][j + 1] : Number.MAX_SAFE_INTEGER;
dp[i][j] = matrix[i][j] + Math.min(top, topLeft, topRight);
}
}
for (let i = 0; i < n; i++) {
res = Math.min(res, dp[n - 1][i]); // 落在最后一行路径和的最小值
}
return res;
};120. 三角形最小路径和
js
/**
* v1 动态规划(dp数组)
* @param {number[][]} triangle
* @return {number}
*/
const minimumTotal = function (triangle) {
const n = triangle.length;
// dp[i][j]表示从triangle[0][0]出发到triangle[i][j]的最小下降路径和
const dp = Array.from({ length: n }, () => new Array(n).fill(Infinity));
// 初始化
dp[0][0] = triangle[0][0];
for (let i = 1; i < n; i++) {
for (let j = 0; j < triangle[i].length; j++) {
const topLeft = j - 1 >= 0 ? dp[i - 1][j - 1] : Infinity;
const top = j < triangle[i - 1].length ? dp[i - 1][j] : Infinity;
dp[i][j] = Math.min(topLeft, top) + triangle[i][j];
}
}
let result = Infinity;
for (const num of dp[n - 1]) {
if (num < result) result = num;
}
return result;
};343. 整数拆分
js
/**
* v1 动态规划(dp数组)
* @param {number} n
* @return {number}
*/
const integerBreak = function (n) {
// 1、明确dp数组和索引的定义
// dp[i]将数字 i 将其拆分为 k 个正整数的和得到的最大乘积。结果:dp[n]
// 2、状态转移方程
// dp[i] = Math.max(dp[i], j * (i - j), j * dp[i - j]), j < i
// 3、初始化
// 4、遍历顺序
const dp = new Array(n + 1).fill(0);
dp[2] = 1;
for (let i = 3; i <= n; i++) {
for (let j = 1; j <= Math.floor(i / 2); j++) {
// 拆分成m个近似相同的子数相乘才是最大的, m >= 2,因此 j 只需要遍历到 i / 2
dp[i] = Math.max(dp[i], j * (i - j), j * dp[i - j]);
}
}
return dp[n];
};96. 不同的二叉搜索树
js
/**
* v2 动态规划(自底向上)
* @param {number} n
* @return {number}
*/
const numTrees = function (n) {
// 1. 确定dp数组和索引的定义
// dp[i]表示给定一个整数 i ,求恰由 i 个节点组成且节点值从 1 到 i 互不相同的二叉搜索树的数量
// 2. 确定状态转移方程
// dp[i] += dp[j - 1] * dp[i - j]
// 3. 初始化
// dp[1] = 1 dp[2] = 2
const dp = new Array(n + 1).fill(0);
dp[0] = 1; // 空子树
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= i; j++) {
// 当 j 为根节点时:
// 左子树由节点 [1, j-1] 组成,共有 j-1 个节点,其形态数为 dp[j-1]
// 右子树由节点 [j+1, i] 组成,共有 i-j 个节点,其形态数为 dp[i-j]
// 根据乘法原理,以 j 为根的 BST 数量 = 左子树形态数 * 右子树形态数
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
};91. 解码方法
js
/**
* v1 动态规划(dp数组)
* @param {string} s
* @return {number}
*/
const numDecodings = function (s) {
const n = s.length;
// dp[i]表示字符串s[0...i-1]的解码方法总数
const dp = new Array(n + 1).fill(0);
// 初始化s 为空或者 s 只有一个字符的情况
dp[0] = 1;
dp[1] = s[0] === "0" ? 0 : 1;
for (let i = 2; i <= n; i++) {
let c = s[i - 1];
let d = s[i - 2];
// 当前消息可以解码
if (c >= "1" && c <= "9") {
dp[i] += dp[i - 1];
}
// 当前消息和前一位消息合并可以解码
if (d === "1" || (d === "2" && c <= "6")) {
dp[i] += dp[i - 2];
}
}
return dp[n];
};背包问题
01 背包
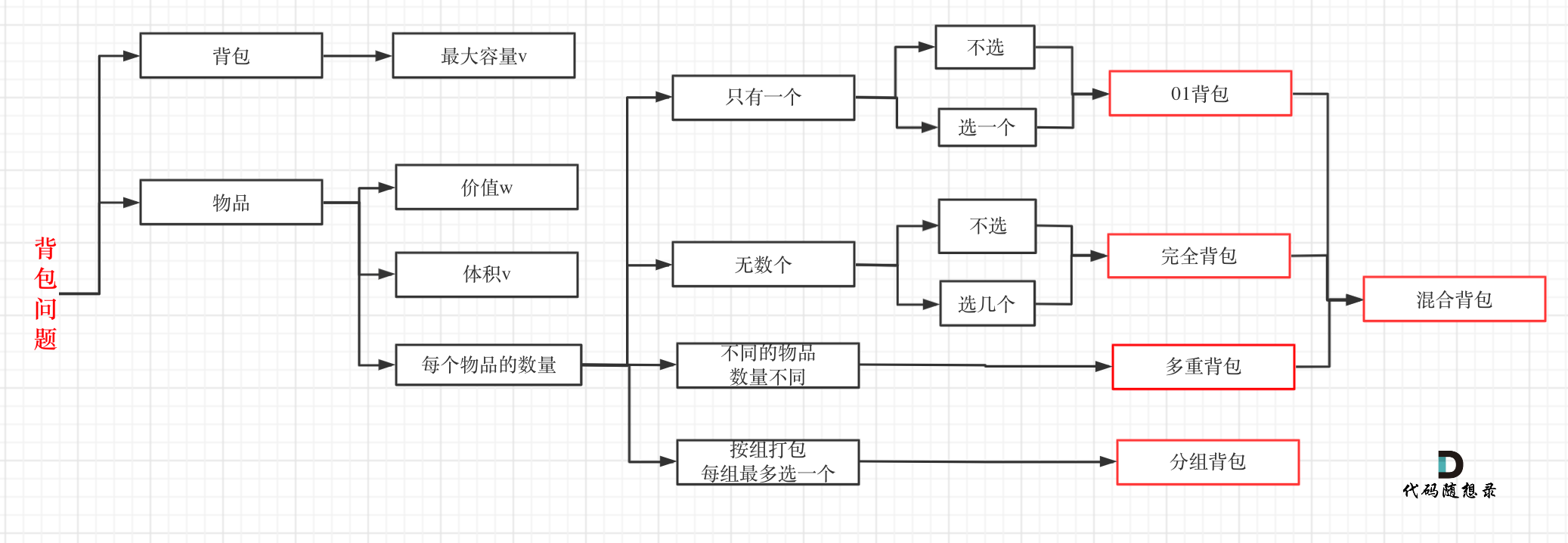
TIP
01 背包问题中 dp 数组从二维降到一维时,需要倒序遍历,避免重复放入物品
416. 分割等和子集 - 是否能够装满背包
js
/**
* v1 动态规划(自底向上)
* @param {number[]} nums
* @return {boolean}
*/
let canPartition = function (nums) {
let sum = nums.reduce((a, b) => a + b);
if (sum % 2 !== 0) return false; // 和为奇数则不可能分割
sum = sum / 2;
let n = nums.length;
// 问题转换:
// 给一个可装载重量为 sum 的背包和 n 个物品,每个物品的重量为 nums[i]。
// 是否存在一种装法,能够恰好将背包装满?
// dp[n][w]:背包可承载的重量为 w 的时候,从前 n 个物品中选取,是否可以装满背包
let dp = Array.from({ length: n + 1 }, () => new Array(sum + 1).fill(false));
// base case
// n = 0 时 dp[n][w] = false 没有物品可选,无法装满(除0容量外)
// w = 0 时 dp[n][w] = true 背包没有容量,视作装满了
for (let i = 0; i <= n; i++) {
dp[i][0] = true;
}
for (let i = 1; i < n + 1; i++) {
for (let j = 1; j < sum + 1; j++) {
// 决策过程:是否选择第 i 个物品(索引为 i-1)
if (nums[i - 1] > j) {
dp[i][j] = dp[i - 1][j]; // 第 i个物品太重,无法装入,只能不装
} else {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]]; // 可以选择装入或不装入,只要有一种能成功就行
}
}
}
return dp[n][sum];
};js
/**
* v2 动态规划(01背包:dp数组)
* @param {number[]} nums
* @return {boolean}
*/
let canPartition = function (nums) {
let sum = nums.reduce((a, b) => a + b);
if (sum % 2 !== 0) return false; // 和为奇数则不可能分割
sum = sum / 2;
let n = nums.length;
// 问题转换:
// 给一个可装载重量为 sum 的背包和 n 个物品,每个物品的重量为 nums[i]。
// 是否存在一种装法,能够恰好将背包装满?
// 定义dp[j]表示当背包容量为j时是否存在一种方法可以装满背包
const dp = new Array(sum + 1).fill(false);
dp[0] = true;
// 先遍历物品
for (let i = 0; i < n; i++) {
// 然后倒叙遍历容量
for (let j = sum; j >= nums[i]; j--) {
dp[j] = dp[j] || dp[j - nums[i]];
}
}
return dp[sum];
};1049. 最后一块石头的重量 II - 背包能够装的最大重量是多少
js
/**
* v1 动态规划(子集背包问题:自底向上)
* @param {number[]} stones
* @return {number}
*/
const lastStoneWeightII = function (stones) {
// 由于石头之间会相互抵消,那么本题求的就是将数组分为两个集合,求两个集合和的最小差值
// 想要差值最小则集合的和应该接近 sum / 2
// 因此问题转换为,给定一个容量为 sum / 2 的背包和重量为stones[i]的物品,请问背包能够装的最大重量是多少
const n = stones.length;
let sum = stones.reduce((a, b) => a + b);
let target = Math.floor(sum / 2);
// 定义: dp[i][j]表示当容量为j时,只使用前i个物品,背包能够装下的最大重量
const dp = Array.from({ length: n + 1 }, () => new Array(target + 1).fill(0));
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= target; j++) {
if (stones[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(
dp[i - 1][j], // 不放
dp[i - 1][j - stones[i - 1]] + stones[i - 1] // 放
);
}
}
}
return sum - dp[n][target] * 2;
};js
/**
* v2 动态规划(子集背包问题:自底向上+空间压缩)
* @param {number[]} stones
* @return {number}
*/
const lastStoneWeightII = function (stones) {
// 由于石头之间会相互抵消,那么本题求的就是将数组分为两个集合,求两个集合和的最小差值
// 想要插值最小则集合的和应该接近 sum / 2
// 因此问题转换为,给定一个容量为 sum / 2 的背包和重量为stones[i]的物品,请问背包能够装的最大重量是多少
const n = stones.length;
let sum = stones.reduce((a, b) => a + b);
let target = Math.floor(sum / 2);
// 定义: dp[j]表示当容量为j时,背包能够装下的最大重量
const dp = new Array(target + 1).fill(0);
// 先遍历物品
for (let i = 0; i < n; i++) {
// 再倒序遍历容量
for (let j = target; j > 0; j--) {
if (stones[i] <= j) {
dp[j] = Math.max(
dp[j], // 不放
dp[j - stones[i]] + stones[i] // 放
);
}
}
}
return sum - dp[target] * 2;
};494. 目标和 - 装满背包有几种方法
js
/**
* v1 动态规划(转换为子集背包问题)
* @param {number[]} nums 非负整数数组
* @param {number} target 目标和(可能为负数)
* @return {number} 返回能达到目标和的表达式数量
*/
let findTargetSumWays = function (nums, target) {
// 把 nums 划分成两个子集 A 和 B,分别代表分配 + 的数和分配 - 的数
// 则 sum(A) - sum(B) = target
// sum(A) = target + sum(B)
// 2 * sum(A) = target + sum(B) + sum(A)
// 2 * sum(A) = target + sum(nums)
// sum(A) = (target + sum(nums)) / 2
// 问题等价于:
// 有一个容量为 (target + sum(nums)) / 2 的背包,
// 现在给你 N 个物品,第 i 个物品的重量为 nums[i - 1],
// 每个物品只有一个,有几种方式能够恰好装满这个背包
let sum = nums.reduce((a, b) => a + b);
// 这两种情况,不可能存在合法的子集划分
if (sum + target < 0 || (sum + target) % 2 === 1) return 0;
sum = (sum + target) / 2;
let n = nums.length;
// dp[i][j]表示使用前i个物品,装满容量为j的背包的方式
let dp = Array.from({ length: n + 1 }, () => new Array(sum + 1).fill(0));
// base case
dp[0][0] = 1; // nums中可以存在0,因此dp[i][0]不能初始化为 1
for (let i = 1; i <= n; i++) {
for (let j = 0; j <= sum; j++) {
if (nums[i - 1] > j) {
// 背包的空间不足,只能选择不装物品 i
dp[i][j] = dp[i - 1][j];
} else {
// 两种选择的结果之和
dp[i][j] = dp[i - 1][j - nums[i - 1]] + dp[i - 1][j];
}
}
}
return dp[n][sum];
};js
/**
* v2 动态规划(子集背包:自底向上+空间压缩)
* @param {number[]} nums 非负整数数组
* @param {number} target 目标和(可能为负数)
* @return {number} 返回能达到目标和的表达式数量
*/
let findTargetSumWays = function (nums, target) {
// 把 nums 划分成两个子集 A 和 B,分别代表分配 + 的数和分配 - 的数
// 则 sum(A) - sum(B) = target
// sum(A) = target + sum(B)
// 2 * sum(A) = target + sum(B) + sum(A)
// 2 * sum(A) = target + sum(nums)
// sum(A) = (target + sum(nums)) / 2
// 问题等价于:
// 有一个容量为 (target + sum(nums)) / 2 的背包,
// 现在给你 N 个物品,第 i 个物品的重量为 nums[i - 1],
// 每个物品只有一个,有几种方式能够恰好装满这个背包
let sum = nums.reduce((a, b) => a + b);
// 这两种情况,不可能存在合法的子集划分
if (sum + target < 0 || (sum + target) % 2 === 1) return 0;
sum = (sum + target) / 2;
let n = nums.length;
// dp[j]表示装满容量为j的背包的方式共有几种
let dp = new Array(sum + 1).fill(0);
// 初始化,想当于初始化二维的dp[0][j],即二维矩阵第一行
dp[0] = 1;
// 先遍历物品
for (let i = 0; i < n; i++) {
// 再倒序遍历容量
// 注意:必须遍历到 nums[i],处理 nums[i] 为 0 的情况
for (let j = sum; j >= nums[i]; j--) {
// 两种选择的结果之和
dp[j] = dp[j - nums[i]] + dp[j];
}
}
return dp[sum];
};474. 一和零 - 背包(多维)能够装的最大重量是多少
js
/**
* v1 动态规划(01背包问题:自底向上)
* @param {string[]} strs
* @param {number} m
* @param {number} n
* @return {number}
*/
const findMaxForm = function (strs, m, n) {
const len = strs.length;
// 定义:dp[i][j][k]表示在给定0和1的个数分别为j和k时,只使用前i个字符串,可以装的最大字符串数
const dp = Array.from({ length: len + 1 }, () =>
Array.from({ length: m + 1 }, () => new Array(n + 1).fill(0))
);
for (let i = 1; i <= len; i++) {
for (let j = 0; j <= m; j++) {
for (let k = 0; k <= n; k++) {
// 计算0和1的数量
const [zeroCount, oneCount] = count(strs[i - 1]);
// 有足够的空间可以装下
if (j >= zeroCount && k >= oneCount) {
// 选择装或者不装
dp[i][j][k] = Math.max(
dp[i - 1][j][k], // 不装
dp[i - 1][j - zeroCount][k - oneCount] + 1 // 装
);
} else {
// 没有足够的空间把当前字符串装进背包
// 只能选择不装
dp[i][j][k] = dp[i - 1][j][k];
}
}
}
}
// 统计字符串中的01个数
function count(str) {
let zeroCount = 0;
const n = str.length;
for (let i = 0; i < n; i++) {
if (str[i] === "0") zeroCount++;
}
return [zeroCount, n - zeroCount];
}
return dp[len][m][n];
};js
/**
* v2 动态规划(01背包问题:自底向上+空间压缩)
* @param {string[]} strs
* @param {number} m
* @param {number} n
* @return {number}
*/
const findMaxForm = function (strs, m, n) {
const len = strs.length;
// 定义:dp[j][k]表示在给定0和1的个数分别为j和k时,可以装的最大字符串数(压缩为2维数组)
const dp = Array.from({ length: m + 1 }, () => new Array(n + 1).fill(0));
for (let i = 0; i < len; i++) {
// 计算0和1的数量
const [zeroCount, oneCount] = count(strs[i]);
// 倒序遍历
for (let j = m; j >= zeroCount; j--) {
for (let k = n; k >= oneCount; k--) {
// 选择装或者不装
dp[j][k] = Math.max(
dp[j][k], // 不装
dp[j - zeroCount][k - oneCount] + 1 // 装
);
}
}
}
// 统计字符串中的01个数
function count(str) {
let zeroCount = 0;
const n = str.length;
for (let i = 0; i < n; i++) {
if (str[i] === "0") zeroCount++;
}
return [zeroCount, n - zeroCount];
}
return dp[m][n];
};完全背包
TIP
完全背包问题可以直接编写一维 dp 数组:
- 如果求组合数就是外层 for 循环遍历物品,内层 for 遍历背包。
- 如果求排列数就是外层 for 遍历背包,内层 for 循环遍历物品。
完全背包-不考虑顺序
518. 零钱兑换 II - 装满背包有几种方法
js
/**
* v1 动态规划(完全背包问题:dp数组)
* @param {number} amount 目标金额
* @param {number[]} coins 不同面额的硬币数组
* @return {number} 返回可以凑成总金额的硬币组合数
*/
let change = function (amount, coins) {
let m = coins.length;
// dp[i][j]表示使用coins中的前 i 个硬币(每种硬币无限个),组合成总金额为 j 的组合数
const dp = Array.from({ length: m + 1 }, () => new Array(amount + 1).fill(0));
// base case dp[0][j] = 0, dp[i][0] = 1
for (let i = 0; i <= m; i++) {
dp[i][0] = 1;
}
// 遍历每种硬币
for (let i = 1; i <= m; i++) {
// 遍历每个金额
for (let j = 1; j <= amount; j++) {
// 如果当前硬币面额大于目标金额,则不能使用该硬币
if (coins[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
// 状态转移方程:
// dp[i-1][j]:不使用第i个硬币的组合数
// dp[i][j-coins[i-1]]:使用第i个硬币的组合数(因为硬币可重复使用,所以是dp[i]而不是dp[i-1])
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]];
}
}
}
return dp[m][amount];
};js
/**
* v1 动态规划(完全背包问题:dp数组+空间压缩)
* @param {number} amount 目标金额
* @param {number[]} coins 不同面额的硬币数组
* @return {number} 返回可以凑成总金额的硬币组合数
*/
let change = function (amount, coins) {
let m = coins.length;
// dp[j]表示组合成总金额为 j 的组合数
const dp = new Array(amount + 1).fill(0);
// 初始化
dp[0] = 1;
// 遍历每种硬币
for (let i = 0; i < m; i++) {
// 遍历每个金额
for (let j = 1; j <= amount; j++) {
if (coins[i] > j) continue;
dp[j] = dp[j] + dp[j - coins[i]];
}
}
return dp[amount];
};322. 零钱兑换 - 装满背包的最少物品数
js
/**
* v1 动态规划(完全背包:自底向上)
* @param {number[]} coins
* @param {number} amount
* @return {number}
*/
let coinChange = function (coins, amount) {
// dp[i][j]使用前i个硬币,凑成总金额为 j 时,需要的最少硬币数
const n = coins.length;
let dp = Array.from({ length: n + 1 }, () =>
new Array(amount + 1).fill(Infinity)
);
// base case
for (let i = 0; i <= n; i++) {
dp[i][0] = 0;
}
// 遍历所有的硬币
for (let i = 1; i <= n; i++) {
const coin = coins[i - 1];
// 遍历总金额
for (let j = 1; j <= amount; j++) {
if (j < coin) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - coin] + 1);
}
}
}
return dp[n][amount] === Infinity ? -1 : dp[n][amount];
};js
/**
* v2 动态规划(完全背包:自底向上+空间压缩)
* @param {number[]} coins
* @param {number} amount
* @return {number}
*/
let coinChange = function (coins, amount) {
// dp[i]代表总金额为 i 时需要的最少硬币数
// 因为最多硬币数量为amount,所以初始化为 amount + 1,相当于初始化为正无穷
let dp = new Array(amount + 1).fill(amount + 1);
// base case
dp[0] = 0;
// 遍历所有的硬币
for (let coin of coins) {
// 遍历总金额
for (let i = 1; i <= amount; i++) {
if (i - coin < 0) continue;
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
return dp[amount] === amount + 1 ? -1 : dp[amount];
};279. 完全平方数 - 装满背包的最少物品数
js
/**
* v1 动态规划(完全背包:自底向上)
* @param {number} n
* @return {number}
*/
const numSquares = function (n) {
const nums = [];
// 找到所有的完全平凡数
for (let i = 1; i * i <= n; i++) {
nums.push(i * i);
}
const len = nums.length;
// 定义:dp[i][j] 表示从前 i 个完全平方数中选,凑出金额 j 的最少数量
const dp = Array.from({ length: len + 1 }, () =>
new Array(n + 1).fill(Infinity)
);
// base case: 凑出金额 0 需要 0 个数
for (let i = 0; i <= len; i++) {
dp[i][0] = 0;
}
// 遍历物品
for (let i = 1; i <= len; i++) {
const num = nums[i - 1]; // 当前物品的重量/面值
// 遍历背包容量
for (let j = 1; j <= n; j++) {
if (j < num) {
// 容量不足,只能不选当前物品,继承前 i-1 个物品的结果
dp[i][j] = dp[i - 1][j];
} else {
// 容量足够,可以选择:
// 1. 不选当前物品:dp[i-1][j]
// 2. 选当前物品:dp[i][j - num] + 1
// 注意:因为是完全背包(物品可重复选),所以选了当前物品后,状态转移到 dp[i] 而不是 dp[i-1]
// 意思是:在当前还可以继续选第 i 个物品的状态下,腾出 num 的空间
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - num] + 1);
}
}
}
return dp[len][n];
};js
/**
* v2 动态规划(完全背包问题:自底向上+空间压缩)
* @param {number} n
* @return {number}
*/
const numSquares = function (n) {
const nums = [];
for (let i = 1; i * i <= n; i++) {
nums.push(i * i);
}
const len = nums.length;
// 定义:dp[i]表示给目标金额i和零钱nums,凑出金额的最少零钱数
const dp = new Array(n + 1).fill(Infinity);
dp[0] = 0;
// 遍历金额
for (let i = 1; i <= n; i++) {
// 遍历零钱
for (let j = 0; j < len; j++) {
if (nums[j] > i) {
continue;
}
// 选择需要零钱最少的那个结果
dp[i] = Math.min(dp[i], dp[i - nums[j]] + 1);
}
}
return dp[n];
};完全背包-考虑顺序
377. 组合总和 Ⅳ - 装满背包有几种方法
js
/**
* v1 动态规划(完全背包求排列:二维数组版本)
*
* 注意:
* 1. 标准的“物品 x 容量”二维数组(dp[i][j])只能计算组合数,无法计算排列数。
* 2. 对于排列问题,二维的定义必须变为:dp[k][j] 表示“使用 k 个物品凑出容量 j 的排列数”。
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
const combinationSum4 = function (nums, target) {
// dp[k][j] 表示:使用 k 个物品凑出容量 j 的排列数
// k 的最大可能长度是 target(假设最小物品是 1)
const dp = Array.from({ length: target + 1 }, () =>
new Array(target + 1).fill(0)
);
// base case: 长度为 0,总和为 0 的方案数为 1
dp[0][0] = 1;
// 遍历序列长度 k
for (let k = 1; k <= target; k++) {
// 遍历当前背包容量
for (let j = 0; j <= target; j++) {
// 遍历每一个物品,尝试将其作为序列的第 k 个元素
for (const num of nums) {
if (j >= num) {
// 如果当前位置放 num,那么前 k-1 个元素必须凑出 j - num
dp[k][j] += dp[k - 1][j - num];
}
}
}
}
// 最终结果是所有可能长度的方案总和
let ans = 0;
for (let k = 1; k <= target; k++) {
ans += dp[k][target];
}
return ans;
};js
/**
* v2 动态规划(完全背包求排列问题:一维数组)
* 注意:本题求的是“排列数”(顺序不同视为不同),而非“组合数”。
* - 求组合数:先遍历物品,再遍历背包(完全背包标准模板)
* - 求排列数:先遍历背包,再遍历物品
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
const combinationSum4 = function (nums, target) {
// dp[i]表示凑出容量为i的背包的排列数
const dp = new Array(target + 1).fill(0);
dp[0] = 1;
// 因为求排列数所以必须先遍历背包容量,再遍历物品
// 这样才能保证对于每个容量,所有物品都有机会作为“最后一个物品”被选中,从而产生不同的排列
// 例如 dp[3] 可以由 dp[2] + 1 (最后选1) 和 dp[1] + 2 (最后选2) 推导而来
// 这就覆盖了 (1, 2) 和 (2, 1) 两种情况
for (let i = 1; i <= target; i++) {
// 后遍历物品
for (const num of nums) {
if (num > i) {
continue;
}
dp[i] += dp[i - num];
}
}
return dp[target];
};爬楼梯进阶版 - 装满背包有几种方法
js
✨139. 单词拆分 - 是否能够装满背包
js
/**
* v1 动态规划(完全背包问题求排列)
* @param {string} s
* @param {string[]} wordDict
* @return {boolean}
*/
const wordBreak = function (s, wordDict) {
const n = s.length;
// dp[i]表示字符串s的前i位是否可以拆分为字典中的一个或多个单词的组合
const dp = new Array(n + 1).fill(false);
dp[0] = true;
// 排列问题
// 先遍历容量(字符串长度)
for (let i = 1; i <= n; i++) {
// 后遍历物品(字典中的单词)
for (const word of wordDict) {
const len = word.length;
// 1. 只有当前截取的长度 i 大于等于单词长度时,才有可能匹配
// 2. 截取 s 的后 len 位,判断是否等于当前 word
// 3. 并且剩余的前半部分 (i - len) 必须也能被拆分 (dp[i - len] 为 true)
if (i >= len && s.slice(i - len, i) === word && dp[i - len]) {
dp[i] = true;
// 只要找到一种匹配方式,当前长度 i 就通过了,无需尝试其他单词
break;
}
}
}
return dp[n];
};打家劫舍
198. 打家劫舍
js
/**
* v1 动态规划(自底向上)
* @param {number[]} nums
* @return {number}
*/
let rob = function (nums) {
const n = nums.length;
if (n === 1) return nums[0];
// dp[i]表示前i个房子中能够偷到的最大金额
const dp = new Array(n + 1).fill(0);
dp[1] = nums[0];
for (let i = 2; i <= n; i++) {
// 偷和不偷第i个房子的两个选择取较大值
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);
}
return dp[n];
};2140. 解决智力问题
js
/**
* v1 动态规划(打家劫舍问题:dp数组)
* @param {number[][]} questions
* @return {number}
*/
const mostPoints = function (questions) {
const n = questions.length;
if (n === 1) return questions[0][0];
// dp[i]表示从questions[i]开始做题,能够获得的最大分数
const dp = new Array(n).fill(0);
dp[n - 1] = questions[n - 1][0];
for (let i = n - 2; i >= 0; i--) {
const skip = dp[i + 1]; // 不做这题
const next = i + questions[i][1] + 1;
const take = questions[i][0] + (next < n ? dp[next] : 0); // 做这题并跳过冷却
dp[i] = Math.max(skip, take);
}
return dp[0];
};740. 删除并获得点数
js
/**
* v1 动态规划(打家劫舍问题:dp数组)
* @param {number[]} nums
* @return {number}
*/
const deleteAndEarn = function (nums) {
const points = new Array(10001).fill(0);
// 建立每个点数和其和的映射
for (const num of nums) {
points[num] += num;
}
// 接下来就相当于打家劫舍问题:
// points中代表每个编号房子的财富,相邻的房子不能偷窃,求可以获得的最大财富。
const n = points.length;
// dp[i]表示从前i个房子中能够偷到的最大金额
const dp = new Array(n + 1).fill(0);
dp[1] = points[0];
for (let i = 2; i <= n; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + points[i - 1]);
}
return dp[n];
};983. 最低票价
js
/**
* v1 动态规划(打家劫舍问题:dp数组)
* @param {number[]} days
* @param {number[]} costs
* @return {number}
*/
const mincostTickets = function (days, costs) {
const n = days.length;
// dp[i]表示完成days[i...]的最低消费
const dp = new Array(n).fill(Infinity);
dp[n - 1] = Math.min(...costs); // 不一点买一天最便宜
for (let i = n - 2; i >= 0; i--) {
// 当前在第days[i]天,考虑买哪种通信证
// 买一天
let buy1 = costs[0] + dp[i + 1];
// 买七天
let freeDays = days[i] + 7 - 1; // 表示可以免费路由直到第freeDays天
let next = i;
while (days[next] <= freeDays) {
next++; // 找到下一次需要重新买通行证对应天数的索引
}
let buy7 = costs[1] + (next < n ? dp[next] : 0);
// 买三十天
freeDays = days[i] + 30 - 1;
next = i;
while (days[next] <= freeDays) {
next++;
}
let buy30 = costs[2] + (next < n ? dp[next] : 0);
dp[i] = Math.min(buy1, buy7, buy30);
}
return dp[0];
};213. 打家劫舍 II
js
/**
* v1 动态规划(自底向上)
* @param {number[]} nums
* @return {number}
*/
let rob = function (nums) {
const n = nums.length;
if (n === 1) return nums[0];
return Math.max(robRange(nums, 0, n - 2), robRange(nums, 1, n - 1));
};
// 参考题[198] 打家劫舍
function robRange(nums, start, end) {
if (start > end) return 0;
if (start === end) return nums[start];
const n = nums.length;
const dp = new Array(n).fill(0);
dp[start] = nums[start];
dp[start + 1] = Math.max(nums[start], nums[start + 1]);
for (let i = start + 2; i <= end; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[end];
}337. 打家劫舍 III
js
/**
* v2 分解问题思想
* @param {TreeNode} root
* @return {number}
*/
let rob = function (root) {
// 返回一个数组arr:
// arr[0]表示抢root,得到的最大钱数
// arr[1]:表示不抢root得到的最大钱数
let _rob = function (root) {
if (root === null) return [0, 0];
let left = _rob(root.left);
let right = _rob(root.right);
/// 抢,下家不可抢
let doIt = root.val + left[1] + right[1];
// 不抢,下家可抢可不抢,取决于收益大小
let notDo = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
return [doIt, notDo];
};
let res = _rob(root);
return Math.max(res[0], res[1]);
};股票问题
股票问题通用解题思路
问题抽象 此类问题的核心是在给定价格序列 prices 中,通过买入和卖出操作(可能受限于交易次数 k、冷冻期或手续费)来最大化利润。
通用状态定义 定义 dp[i][k][s] 为:第 i 天,至多进行 k 次交易,当前持有状态为 s(0 表示不持有,1 表示持有)时的最大利润。
状态转移方程
- 今天不持有 (
s=0):dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])解释:要么昨天就不持有(休息),要么昨天持有今天卖出(套现)。
- 今天持有 (
s=1):dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])解释:要么昨天就持有(休息),要么昨天不持有今天买入(投资)。 注:通常在买入时扣减交易次数 k,也可以在卖出时扣减,保持一致即可。
常用技巧
- 状态压缩(状态机):由于
dp[i]只依赖dp[i-1],可将空间从 $O(N)$ 优化为 $O(1)$,仅用变量维护当天的状态(如buy,sell)。 - 初始化:
dp[0][...][1]通常初始化为-prices[0],dp[0][...][0]初始化为 0。
121. 买卖股票的最佳时机 - 只能买卖一次
js
/**
* v1 贪心算法
* 时间复杂度:O(n)
* 空间复杂度:O(1)
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
// 因为股票只能买卖一次,那么贪心的想法很自然就是取最左最小值,取最右最大值,
// 那么得到的差值就是最大利润。
let low = Number.MAX_SAFE_INTEGER;
let result = 0;
for (const price of prices) {
low = Math.min(low, price); // 取最左最小价格
result = Math.max(result, price - low); // 取最大区间利润
}
return result;
};js
/**
* v1 动态规划(股票问题:状态机)
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
let n = prices.length;
// 初始化第0天
let buy1 = -prices[0]; // 目前已经完成一次买入后的最大利润
let sell1 = 0; // 目前已经完成一次卖出后的最大利润
// 遍历每一天
for (let i = 1; i < n; i++) {
// 更新状态
buy1 = Math.max(buy1, -prices[i]); // 之前已经买入了或者今天买入
sell1 = Math.max(sell1, buy1 + prices[i]); // 之前已经卖出了或者今天卖出
}
return sell1;
};js
/**
* v1 动态规划(自底向上)
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
let n = prices.length;
// 1 表示持有股票,0 表示不持有股票
// dp[i][1]或者dp[i][0],分别表示在第i天时对应的最大利润
let dp = Array.from({ length: n }, () => new Array(2).fill(0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (let i = 1; i < n; i++) {
//第i天不持有股票: i - 1天不持有股票、第i - 1天持有股票,但是第i天卖了
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
// 第i天持有股票:i - 1天持有股票;第i天第一次买入(注意:只能买一次,所以买入时的本金是0,而不是之前的利润)
dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
}
return dp[n - 1][0];
};122. 买卖股票的最佳时机 II - 可以进行多次买卖
js
/**
* v1 贪心算法
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
// 计算每天股票的利润的序列,通过收集所有的正利润
let result = 0;
for (let i = 1; i < prices.length; i++) {
result += Math.max(prices[i] - prices[i - 1], 0);
}
return result;
};js
/**
* v1 动态规划(状态机)
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
let n = prices.length;
if (n === 0 || n === 1) return 0;
// 初始化(第0天)
let hold = -prices[0]; // 当天持有股票的最大利润
let rest = 0; // 当天不持有股票的最大利润
for (let i = 1; i < n; i++) {
let prevHold = hold;
let prevRest = rest;
// 当天持有股票的状态:
// 1. 前一天持有股票
// 2. 前一天不持有股票+当天买入股票
hold = Math.max(prevHold, prevRest - prices[i]);
// 当天不持有股票的状态:
// 1. 前一天不持有股票
// 2. 前一天持有股票+当天卖出股票
rest = Math.max(prevRest, prevHold + prices[i]);
}
return rest;
};js
/**
* v1 动态规划(自底向上)
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
let n = prices.length;
// 1 表示持有股票,0 表示不持有股票
// dp[i][1]或者dp[i][0],分别表示在第i天时对应的最大利润
let dp = Array.from({ length: n }, () => new Array(2).fill(0));
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (let i = 1; i < n; i++) {
// 第i天不持有股票: i - 1天不持有股票或者第i - 1 天持有股票,但是第i天卖了
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
// 第i天持有股票:i - 1天持有股票或者第i - 1天不持有股票,但是第i天买了
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
};123. 买卖股票的最佳时机 III - 最多进行 2 次买卖
js
/**
* v1.1 动态规划(状态机)
*/
const maxProfit = function (prices) {
// 1. 目前已经完成一次买入后的最大利润 (buy1)
// 2. 目前已经完成一次卖出后的最大利润 (sell1)
// 3. 目前已经完成两次买入后的最大利润 (buy2)
// 4. 目前已经完成两次卖出后的最大利润(sell2)
// 初始化(第0天)
let buy1 = -prices[0]; // 买入股票
let sell1 = 0; // 买了又卖
let buy2 = -prices[0]; // 买了又卖又买
let sell2 = 0; // 进行了两次买卖操作
for (let i = 1; i < prices.length; i++) {
// 顺序更新 4 个状态
// 目前已经完成一次买入后的最大利润:要么之前就买了,要么今天刚买
buy1 = Math.max(buy1, -prices[i]);
// 目前已经完成一次卖出后的最大利润:要么之前就卖了,要么今天卖
sell1 = Math.max(sell1, buy1 + prices[i]);
// 目前已经完成两次买入后的最大利润:要么之前就买了,要么今天刚买
buy2 = Math.max(buy2, sell1 - prices[i]);
// 目前已经完成两次卖出后的最大利润:要么之前就卖了,要么今天卖
sell2 = Math.max(sell2, buy2 + prices[i]);
}
return sell2;
};js
/**
* v1 动态规划
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
let n = prices.length;
// 定义状态:
// dp[i][k][0]: 第 i 天,至多进行了 k 次交易,且当前【不持有】股票(卖出状态)
// dp[i][k][1]: 第 i 天,至多进行了 k 次交易,且当前【持有】股票(买入状态)
let dp = Array.from({ length: n }, () =>
Array.from({ length: 3 }, () => new Array(2).fill(0))
);
// 初始化
for (let k = 1; k <= 2; k++) {
dp[0][k][0] = 0;
dp[0][k][1] = -prices[0]; // 第一天买入,成本为 prices[0]
}
for (let i = 1; i < n; i++) {
for (let k = 1; k <= 2; k++) {
// 状态转移方程解释:
// 1. 今天【不持有】股票 (dp[i][k][0])
// 可能性 A: 昨天就不持有 (dp[i-1][k][0]) -> 保持现状
// 可能性 B: 昨天持有,今天卖出了 (dp[i-1][k][1] + prices[i]) -> 完成了一次交易
dp[i][k][0] = Math.max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]);
// 2. 今天【持有】股票 (dp[i][k][1])
// 可能性 A: 昨天就持有 (dp[i-1][k][1]) -> 保持现状
// 可能性 B: 昨天不持有,今天买入了 (dp[i-1][k-1][0] - prices[i]) -> 开始第 k 次交易
// 注意:买入是交易的开始,所以我们要从 k-1 (上一轮交易完成) 的状态转移过来
dp[i][k][1] = Math.max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]);
}
}
// 返回最后一天,至多交易 2 次,且不持有股票的最大利润
return dp[n - 1][2][0];
};188. 买卖股票的最佳时机 IV - 最多进行 k 次买卖
js
/**
* v1 动态规划(股票问题:状态机)
* @param {number} k
* @param {number[]} prices
* @return {number}
*/
const maxProfit = function (k, prices) {
const n = prices.length;
// 边界条件处理
if (k === 0 || n === 0) return 0;
// 初始化(假设第 0 天就完成了所有操作)
// buys[j] 表示“目前已经完成了第 j+1 次买入操作”后的最大余额
// 此时处于【持仓】状态
const buys = new Array(k).fill(-prices[0]);
// sells[j] 表示“目前已经完成了第 j+1 次卖出操作”后的最大余额(利润)
// 此时处于【空仓】状态
const sells = new Array(k).fill(0);
// 从第 1 天开始遍历
for (let i = 1; i < n; i++) {
// 每一天都可以尝试更新第 1 次到第 k 次交易的状态
for (let j = 0; j < k; j++) {
// 1. 更新 buys[j] (目标:达到“完成第 j+1 次买入”的状态)
if (j === 0) {
// 第一次买入:
// 选项A: 维持之前的状态(之前早就买好了,今天不动)
// 选项B: 今天刚买入(基于 0 元本金)
buys[j] = Math.max(buys[j], -prices[i]);
} else {
// 第 j+1 次买入:
// 选项A: 维持之前的状态(之前早就买好了)
// 选项B: 今天刚买入(用上一轮“完成第 j 次卖出”后的钱 sells[j-1] 来买)
buys[j] = Math.max(buys[j], sells[j - 1] - prices[i]);
}
// 2. 更新 sells[j] (目标:达到“完成第 j+1 次卖出”的状态)
// 选项A: 维持之前的状态(之前早就卖完了,今天不动,利润不变)
// 选项B: 今天刚卖出(把当前“完成第 j+1 次买入”后的股票 buys[j] 卖掉)
sells[j] = Math.max(sells[j], buys[j] + prices[i]);
}
}
// 返回“截止到最后一天,至多完成了 k 次卖出操作”后的最大利润
return sells[k - 1];
};309. 买卖股票的最佳时机含冷冻期
js
/**
* v1 动态规划(状态机)
* @param {number[]} prices
* @return {number}
*/
const maxProfit = function (prices) {
const n = prices.length;
if (n === 0) return 0;
// 初始化(第0天)
let hold = -prices[0]; // 当天结束时持有股票的最大利润
let sold = 0; // 当天刚卖出(进入冷冻期)的最大利润
let rest = 0; // 当天不持有(包含冷冻期)的最大利润
for (let i = 1; i < n; i++) {
const prevHold = hold;
const prevSold = sold;
const prevRest = rest;
// 当天持有股票:
// 1. 前一天持有股票
// 2. 前一天不持有股票(包含冷冻期)+当天买入股票
hold = Math.max(prevHold, prevRest - prices[i]);
// 当天卖出股票:
// 前一天持有股票+当天卖出
sold = prevHold + prices[i];
// 当天不持有股票(包含冷冻期)
// 1. 前一天不持有股票(包含冷冻期)
// 2. 前一天卖出股票
rest = Math.max(prevRest, prevSold);
}
// 最大值为不持有状态
return Math.max(sold, rest);
};js
/**
* v1 动态规划(dp数组)
* @param {number[]} prices
* @return {number}
*/
const maxProfit = function (prices) {
const n = prices.length;
if (n === 0 || n === 1) return 0;
// 1表示持有股票,0表示不持有股票,dp[i][1]和dp[i][0]表示到i天为止获得的最大利润
const dp = Array.from({ length: n }, () => new Array(2).fill(0));
dp[0][1] = -prices[0];
dp[1][0] = Math.max(0, prices[1] - prices[0]);
dp[1][1] = Math.max(-prices[0], -prices[1]);
for (let i = 2; i < n; i++) {
// 第i天不持有股票的状态:第i-1天不持有股票或者第i-1天持有股票,第i天卖出
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
// 第i天持有股票的状态:第i-1天持有股票或者第i-2天卖出股票进入冷冻期第i天买入股票
// 因为dp[i-1][0]包含两种状态,即第i-1天为冷冻期或者刚卖出的状态,避免包含昨天卖出买入的非法状态所以需要强制隔一天
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - prices[i]);
}
return dp[n - 1][0];
};714. 买卖股票的最佳时机含手续费
js
/**
* v1 动态规划(状态机)
* @param {number[]} prices
* @param {number} fee
* @return {number}
*/
const maxProfit = function (prices, fee) {
const n = prices.length;
if (n === 0 || n === 1) return 0;
// 初始化(第0天)
let hold = -prices[0]; // 当天持有的最大利润
let rest = 0; // 当天不持有的最大利润
for (let i = 1; i < n; i++) {
let prevHold = hold;
let prevRest = rest;
// 当天持有的状态:
// 1. 前一天持有
// 2. 前一天不持有+当天买入
hold = Math.max(prevHold, prevRest - prices[i]);
// 当天不持有的状态:
// 1. 前一天不持有
// 2. 前一天持有+当天卖出(卖出需要交手续费)
rest = Math.max(prevRest, prevHold + prices[i] - fee);
}
return rest;
};子序列问题
300. 最长递增子序列
js
/**
* v1 动态规划(子序列问题)
* @param {number[]} nums
* @return {number}
*/
let lengthOfLIS = function (nums) {
// 定义 dp[i] 表示以nums[i]结尾的最长递增子序列的长度
let dp = new Array(nums.length).fill(1);
// base case:dp 数组全都初始化为 1
for (let i = 1; i < nums.length; i++) {
for (let j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
// 把 nums[i] 接在后面,即可形成长度为 dp[j] + 1,
// 且以 nums[i] 为结尾的递增子序列
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
return Math.max(...dp);
};✨673. 最长递增子序列的个数
js
/**
* v1 动态规划(子序列问题:dp数组)
* @param {number[]} nums
* @return {number}
*/
const findNumberOfLIS = function (nums) {
const n = nums.length;
if (n === 1) return n;
// dp[i]表示以nums[i]结尾的最长递增子序列的长度
const dp = new Array(n).fill(1);
// count[i]表示以nums[i]结尾的最长递增子序列的个数
const count = new Array(n).fill(1);
let maxLen = 1; // 记录最长子序列的长度
for (let i = 1; i < n; i++) {
for (let j = 0; j < i; j++) {
// 只能从更小的数 nums[j] 转移到 nums[i](保持递增)
if (nums[j] < nums[i]) {
// 如果通过 j 延长能得到更长的长度:更新 dp[i],并将计数同步为以 j 结尾的方案数
if (dp[i] < dp[j] + 1) {
dp[i] = dp[j] + 1;
count[i] = count[j];
} else if (dp[i] === dp[j] + 1) {
// 如果通过 j 延长得到的长度恰好等于当前最佳长度:
// 说明存在多条不同路径达到同一长度,累加方案数
count[i] = count[i] + count[j];
}
// 同步维护全局最长长度
maxLen = Math.max(maxLen, dp[i]);
}
}
}
let result = 0;
for (let i = 0; i < n; i++) {
// 统计所有以 i 结尾且长度达到全局最长的方案数
if (dp[i] === maxLen) result += count[i];
}
return result;
};674. 最长连续递增序列
js
/**
* v1 动态规划
* @param {number[]} nums
* @return {number}
*/
const findLengthOfLCIS = function (nums) {
const n = nums.length;
if (n === 0 || n === 1) return n;
// dp[i]表示以nums[i]结尾的连续递增子序列的最大长度
const dp = new Array(n).fill(1);
for (let i = 1; i < n; i++) {
if (nums[i - 1] < nums[i]) {
dp[i] = Math.max(dp[i], dp[i - 1] + 1);
}
}
return Math.max(...dp);
};js
/**
* v1 贪心策略
* @param {number[]} nums
* @return {number}
*/
const findLengthOfLCIS = function (nums) {
const n = nums.length;
if (n === 0 || n === 1) return n;
let result = 0;
let start = 0;
for (let i = 0; i < n; i++) {
// 不再单调后更新起始节点
if (i >= 1 && nums[i - 1] >= nums[i]) {
start = i;
}
// 跟新最大长度
result = Math.max(result, i - start + 1);
}
return result;
};✨1218. 最长定差子序列
js
/**
* v1 动态规划(子序列问题:dp数组)
* @param {number[]} arr
* @param {number} difference
* @return {number}
*/
const longestSubsequence = function (arr, difference) {
const n = arr.length;
if (n === 1) return n;
// dp[i]表示以arr[i]结尾的最长定差子序列的长度
const dp = new Array(n).fill(1);
let maxLen = 1; // 记录最长定差子序列的长度
for (let i = 1; i < n; i++) {
for (let j = 0; j < i; j++) {
if (arr[i] - arr[j] === difference) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
maxLen = Math.max(maxLen, dp[i]);
}
}
return maxLen;
};js
/**
* v1 动态规划(子序列问题:哈希表)
* @param {number[]} arr
* @param {number} difference
* @return {number}
*/
const longestSubsequence = function (arr, difference) {
const n = arr.length;
if (n <= 1) return n;
const dp = new Map(); // dp.get(x)对应以 x 结尾的最长定差子序列长度
let maxLen = 1; // 记录最长定差子序列的长度
// 遍历数组,更新以 x 结尾的最长定差子序列的长度
for (const x of arr) {
// 寻找以 x - difference 结尾的最长定差子序列的长度
const prev = dp.get(x - difference) || 0;
const cur = prev + 1;
// 当前以x结尾的最长定差子序列的长度
const existed = dp.get(x) || 1;
// 更新以x结尾的最长定差子序列的长度
if (cur > existed) dp.set(x, cur);
// 更新最大值
if (cur > maxLen) maxLen = cur;
}
return maxLen;
};✨1027. 最长等差数列
js
/**
* v1 动态规划(子序列问题:哈希表)
* @param {number[]} nums
* @return {number}
*/
const longestArithSeqLength = function (nums) {
const n = nums.length;
if (n <= 1) return n;
// dp[j]表示以nums[j]结尾的,不同差值对应的最长等差子序列的长度
const dp = Array.from({ length: n }, () => new Map());
let res = 2; // n >= 2
for (let i = 0; i < n; i++) {
for (let j = 0; j < i; j++) {
const d = nums[i] - nums[j]; // 计算差值
const prev = dp[j].get(d) || 1; // 对应差值的最长子序列的长度
const cur = prev + 1;
const existed = dp[i].get(d) || 1;
// 更新dp
dp[i].set(d, Math.max(cur, existed));
// 更新最大值
res = Math.max(res, dp[i].get(d));
}
}
return res;
};✨646. 最长数对链
js
/**
* v1 贪心算法
* @param {number[][]} pairs
* @return {number}
*/
const findLongestChain = function (pairs) {
const n = pairs.length;
if (n === 0) return 0;
// 按右端点升序排序,贪心选择最早结束的区间以留出更多后续空间
pairs.sort((a, b) => a[1] - b[1]);
let res = 0;
// 当前链最后一个区间的右端点,初始化为负无穷以便首个区间被选择
let end = -Infinity;
for (const [a, b] of pairs) {
// 若当前区间起点大于上一个选中区间的终点,则可以接入链
if (a > end) {
res++;
end = b;
}
}
return res;
};js
/**
* v2 动态规划(子序列问题:dp数组)
* @param {number[][]} pairs
* @return {number}
*/
const findLongestChain = function (pairs) {
const n = pairs.length;
// 按照升序排序(左右端点都行,只要保证合法前驱 j 被放在 i 之前)
pairs.sort((a, b) => a[0] - b[0]);
// dp[i] 表示以第 pairs[i] 个数对结尾的最长数对链长度。
const dp = new Array(n).fill(1);
let res = 1;
for (let i = 1; i < n; i++) {
for (let j = 0; j < i; j++) {
if (pairs[j][1] < pairs[i][0]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
res = Math.max(res, dp[i]);
}
return res;
};718. 最长重复子数组
js
/**
* v1 动态规划(子序列问题)
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number}
*/
const findLength = function (nums1, nums2) {
const m = nums1.length;
const n = nums2.length;
if (m === 0 || n === 0) return 0;
// dp[i][j]表示以nums1[i - 1]和nums2[j - 1]结尾的公共最长子数组的长度
const dp = Array.from({ length: m + 1 }, () => new Array(n + 1).fill(0));
let maxLen = 0;
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (nums1[i - 1] === nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
// 更新最大值
maxLen = Math.max(maxLen, dp[i][j]);
}
}
}
return maxLen;
};1143. 最长公共子序列
js
/**
* v1 动态规划(子序列问题:dp数组)
* @param {string} text1
* @param {string} text2
* @return {number}
*/
let longestCommonSubsequence = function (text1, text2) {
const m = text1.length;
const n = text2.length;
if (m === 0 || n === 0) return 0;
// dp[i][j]表示text1[0...i-1]和text2[0...j-1]的最长公共子序列的长度
const dp = Array.from({ length: m + 1 }, () => new Array(n + 1).fill(0));
let maxLen = 0;
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (text1[i - 1] === text2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
// 更新最大值
maxLen = Math.max(maxLen, dp[i][j]);
}
}
return maxLen;
};1035. 不相交的线
js
/**
* v1 动态规划(子序列问题:dp数组)
*
* 相当于求两个数组中最长公共子序列的长度(1143. 最长公共子序列)
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number}
*/
const maxUncrossedLines = function (nums1, nums2) {
const m = nums1.length;
const n = nums2.length;
if (m === 0 || n === 0) return 0;
// dp[i][j]表示nums[0...i-1]和nums2[0...j - 1]的最长公共子序列的长度
const dp = Array.from({ length: m + 1 }, () => new Array(n + 1).fill(0));
let maxLen = 0;
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (nums1[i - 1] === nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
maxLen = Math.max(maxLen, dp[i][j]);
}
}
return maxLen;
};53. 最大子数组和
js
/**
* v1 动态规划(子序列问题:dp数组)
* @param {number[]} nums
* @return {number}
*/
let maxSubArray = function (nums) {
let n = nums.length;
if (n === 1) return nums[0];
// dp[i]表示以nums[i]结尾的连续子数组的最大和
const dp = new Array(n).fill(-Infinity);
dp[0] = nums[0];
for (let i = 1; i < n; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
}
return Math.max(...dp);
};js
/**
* v1 前缀和
* 以 nums[i]结尾的最小子数组和 = preNum[i + 1] - min(preNum[0],...,preNum[i])
* @param {number[]} nums
* @return {number}
*/
let maxSubArray = function (nums) {
let n = nums.length;
let preNum = new Array(n);
preNum[0] = 0;
for (let i = 1; i <= n; i++) {
preNum[i] = preNum[i - 1] + nums[i - 1];
}
let minValue = Infinity;
let maxSum = -Infinity;
for (let i = 0; i < n; i++) {
// 维护 minVal 是 preSum[0],...,preSum[i] 的最小值
minValue = Math.min(minValue, preNum[i]);
// preNum[i + 1] - minValue 表示以nums[i]结尾的最大子数组和
maxSum = Math.max(maxSum, preNum[i + 1] - minValue);
}
return maxSum;
};115. 不同的子序列
js
/**
* v1 动态规划(子序列问题:dp)
* @param {string} s
* @param {string} t
* @return {number}
*/
const numDistinct = function (s, t) {
const m = s.length;
const n = t.length;
// dp[i][j]表示s[0..i - 1]的子序列中t[0..j-1] 出现的次数为
const dp = Array.from({ length: m + 1 }, () => new Array(n + 1).fill(0));
// 初始化
for (let i = 0; i <= m; i++) {
dp[i][0] = 1; // 空串是所有字符串的子序列
}
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (s[i - 1] === t[j - 1]) {
// s和t的当前字符相等的时候,可以选择将s和t都前移,也可以选择只前移s,t不前移,个数就是两者相加
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
} else {
// s和t的当前字符不相等的时候,显然要前移s,看s的下一个字符是否和t的当前字符相等
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[m][n];
};583. 两个字符串的删除操作
js
/**
* v1 动态规划(子序列问题:dp数组)
* @param {string} word1
* @param {string} word2
* @return {number}
*/
var minDistance = function (word1, word2) {
let m = word1.length;
let n = word2.length;
// dp[i][j]表示使得word1[...i-1]和word2[...j-1]相等的最小删除步数
const dp = Array.from({ length: m + 1 }, () => new Array(n + 1).fill(0));
// 初始化
for (let i = 0; i <= m; i++) {
dp[i][0] = i;
}
for (let j = 0; j <= n; j++) {
dp[0][j] = j;
}
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (word1[i - 1] === word2[j - 1]) {
// 不需要删,匹配前面的字符
dp[i][j] = dp[i - 1][j - 1];
} else {
// 要么删word1[i - 1]要么删word2[j - 1],删除次数 + 1
dp[i][j] = Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
}
}
}
return dp[m][n];
};72. 编辑距离
js
/**
* v1 动态规划(自底向上)
* @param {string} word1
* @param {string} word2
* @return {number}
*/
let minDistance = function (word1, word2) {
let m = word1.length;
let n = word2.length;
// 定义 dp[i][j]为将s1[0,...,i-1]转换为s2[0,...,j-1]的最小操作数
let dp = Array.from({ length: m + 1 }, () => new Array(n + 1)); // 注意dp数组的尺寸
// base case 初始化
for (let i = 0; i <= n; i++) {
dp[0][i] = i;
}
for (let i = 0; i <= m; i++) {
dp[i][0] = i;
}
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
if (word1[i - 1] === word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(
dp[i - 1][j] + 1, // 删除
dp[i - 1][j - 1] + 1, // 替换
dp[i][j - 1] + 1 // 插入
);
}
}
}
return dp[m][n];
};✨647. 回文子串
js
/**
* v1 动态规划(子序列问题:dp数组)
* @param {string} s
* @return {number}
*/
const countSubstrings = function (s) {
const n = s.length;
if (n === 0 || n === 1) return n;
// dp[i][j]表示s[i...j]是否为回文字串
const dp = Array.from({ length: n }, () => new Array(n).fill(false));
// 初始化(可省略)
for (let i = 0; i < n; i++) {
dp[i][i] = true;
}
let result = 0;
// 注意遍历顺序,取决于递推公式
for (let i = n - 1; i >= 0; i--) {
for (let j = i; j < n; j++) {
if (s[i] === s[j]) {
// 两头相同
// 1. i === j 表示只有一个字符:是回文串
// 2. j === i + 1表示有两个相同字符:是回文串
// 3. j - i > 1 是否为回文串取决于dp[i+1][j-1]是否为回文串
if (i === j || j === i + 1) {
dp[i][j] = true;
result++;
} else if (dp[i + 1][j - 1]) {
// dp[i][j]依赖左下角的dp[i + 1][j - 1],由此确定遍历顺序应该从下到上从左到右
dp[i][j] = true;
result++;
}
} else {
// 两头不同一定不是回文串
dp[i][j] = false;
}
}
}
return result;
};✨1312. 让字符串成为回文串的最少插入次数
js
/**
* v1 动态规划(子序列问题:dp数组)
* @param {string} s
* @return {number}
*/
let minInsertions = function (s) {
let n = s.length;
// dp[i][j]表示s[i,...,j]成为回文串的最小操作次数
let dp = Array.from({ length: n }, () => new Array(n).fill(0));
// 反向遍历
for (let i = n - 1; i >= 0; i--) {
for (let j = i + 1; j < n; j++) {
if (s[i] === s[j]) {
dp[i][j] = dp[i + 1][j - 1];
} else {
dp[i][j] = Math.min(dp[i + 1][j] + 1, dp[i][j - 1] + 1);
}
}
}
return dp[0][n - 1];
};✨516. 最长回文子序列
js
/**
* v1 动态规划(子序列问题:dp数组)
* @param {string} s
* @return {number}
*/
let longestPalindromeSubseq = function (s) {
let n = s.length;
// dp[i][j]为s[i,...,j]中的最长回文子序列的长度
let dp = Array.from({ length: n }, () => new Array(n).fill(0));
// base case dp[i][j] = 1 (i === j)
for (let i = 0; i < n; i++) {
dp[i][i] = 1;
}
// 遍历顺序取决于递推公式
// dp[i][j]依赖于左下角的状态,因此需要从下往上,从左往右遍历
for (let i = n - 1; i >= 0; i--) {
// 这里j=i+1是因为j=i的情况已经初始化过了
for (let j = i + 1; j < n; j++) {
// 状态转移方程
if (s[i] === s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2; // 它俩一定在最长回文子序列中
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]); // 比较 s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长
}
}
}
return dp[0][n - 1];
};